====== Breitensuche (breadth first search, bfs) ======
Es gibt verschiedene Möglichkeit, einen vorgegebenen Graphen ausgehend von einem gegebenen Startknoten systematisch zu durchlaufen, so dass am Ende alle vom Startknoten aus erreichbaren Knoten abgegangen sind. Eine davon ist die **Breitensuche** (engl.: breadth first search, kurz: bfs). Sie geht - vereinfacht beschrieben - nach folgendem Plan vor:
* 1. Besuche alle vom Startknoten genau eine Kante entfernten Knoten, die noch nicht besucht worden sind. \\ -> Beschrifte sie mit 1.
* 2. Besuche alle von den mit 1 beschrifteten Knoten genau eine Kante entfernten Knoten, die noch nicht besucht worden sind. \\ -> Beschrifte sie mit 2.
* 3. Besuche alle von den mit 2 beschrifteten Knoten genau eine Kante entfernten Knoten, die noch nicht besucht worden sind. \\ -> Beschrifte sie mit 3.
* Und so weiter...
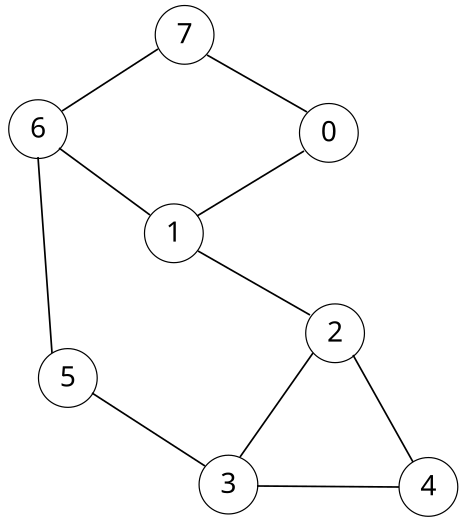
Auf diesem Bild kannst Du gut sehen, in welcher Reihenfolge die Knoten besucht werden.
{{ :graphen:breitensuche:pasted:20231013-115855.png?400 }}
** Interessanter Aspekt: Kürzesten Weg finden** \\
Geht man davon aus, dass jede Kante die Länge 1 hat, so entspricht die Beschriftung der Knoten am Ende der Breitensuche genau ihrer **kürzesten Entfernung zum Startknoten**. Will man also den kürzesten Weg vom Startknoten zu einem vorgegebenen Zielknoten finden, so sucht man - ausgehend vom Startknoten - nach dem Algorithmus der Breitensuche. Sobald der Zielknoten gefunden ist, geht man einfach den Weg rückwärts zu dem Knoten mit der jeweils um 1 niedrigeren Beschriftung. Das ist dann ein kürzester Weg vom Startknoten zum Zielknoten (es kann natürlich mehrere gleich lange Wege geben).
Eine anschauliche Erklärung, wie man sich die Reihenfolge der besuchten Knoten bei der Breitensuche vorstellen kann, finden Sie im 2. Kapitel des folgenden Videos (etwa ab 0:45 min):
{{ youtube>xlVX7dXLS64?large }}
===== Aufgabe 1 =====
{{ :graphen:breitensuche:pasted:20231018-104056.png?300 }}
Der oben gezeichnete Graph soll von A ausgehend mit dem Algorithmus der Breitensuche durchlaufen werden. Geben Sie eine mögliche Reihenfolge der besuchten Knoten an!
[[.aufgabe1Loesung:start|Lösung]]
===== Algorithmus zur Breitensuche =====
{{ youtube>hR4s2W7Dsss?large }}
\\
Der Algorithmus der Breitensuche lässt sich am einfachsten in einem [[https://de.wikipedia.org/wiki/Programmablaufplan|Flussdiagramm]] darstellen:
{{ :graphen:breitensuche:pasted:20231013-132240.png?500 }}
Damit Sie den obigen Algorithmus ganz sicher durchdringen, überdenken Sie ihn kurz im Hinblick auf die drei möglichen Zustände jedes Knotens
- noch nicht besucht
- besucht und in der Warteschlange befindlich
- besucht und nicht mehr in der Warteschlange befindlich
Beschreiben Sie, worin sich der zweite und dritte Zustand unterscheiden.

===== Aufgabe 2 =====
Der Algorithmus zur Breitensuche kann auf einfache Art so abgewandelt werden, dass sich damit ermitteln lässt, ob ein **ungerichteter** Graph zusammenhängend ist oder nicht. Scheibe - ausgehend vom oben gegebenen Programm - eine Methode ''istZusammenhängend'', die genau dann ''true'' zurückgibt, wenn der in der Adjazenzmatrix gespeicherte Graph zusammenhängend ist. \\ \\
Sie können als Ausgangspunkt das folgende Programmfragment benutzen:
[[.aufgabe2Loesung:start|Lösung]]
===== Kürzester Weg zwischen zwei Punkten =====
Um den kürzesten Weg zwischen zwei Punkten nicht nur zu finden, sondern auch auszugeben, reicht es nicht, den Algorithmus zur Breitensuche beim Startknoten zu beginnen und bei Erreichen des Zielknotens zu beenden. Zusätzlich müssen wir für jeden dazwischen erreichten Knoten seinen "Abstand" zum Startknoten speichern und nach Erreichen des Zielknotens in Richtung fallender Abstände die Kanten rückwärts durchlaufen.
Hier wieder eine Skizze dieses Algorithmus als Flussdiagramm:
{{ :graphen:breitensuche:kuerzesterweg.png?600 |}}
Die Interessierten unter Ihnen finden [[.shortestPath:start|hier die Implementierung dieses Algorithmus in Java]].
===== Exkurs zu Game Development: Lee's Algorithm =====
Haben Sie sich schon mal gefragt, wie die Gegner in Computerspielen durch ein Wirrwarr von Labyrinthen immer den kürzesten Weg zur Spielerfigur finden? Dahinter steckt meist Lee's Algorithms, eine Variante der Breitensuche. [[.lee:start|Hier finden Sie ein ausgearbeitetes Beispiel]], in dem dieser Algorithmus erklärt wird.
{{ :graphen:breitensuche:pasted:20231018-133455.png?400 }}

