Stellen wir uns ein Bibliotheksprogramm vor, das verschiedene Listen ausgeben kann:

• eine Liste aller Bücher der Bibliothek
• eine Liste aller Ausleiher/innen
• eine Liste aller säumigen Ausleiher/innen
• usw.

Das Bibliotheksprogramm wird eine Klasse Listenausgabe haben, die für jede der obigen Listen eine Methode besitzt.
Von einem guten Programm würden wir erwarten, dass es diese Listen auf dem Bildschirm, als pdf-Datei, als Html-Datei oder als csv-Datei (zur Verwendung in Tabellenkalkulationen) ausgeben kann. Es müsste also jede der obigen Methoden mehrfach geben:

• eine Liste aller Bücher der Bibliothek auf dem Bildschirm ausgeben
• eine Liste aller Bücher der Bibliothek als pdf-Datei ausgeben
• eine Liste aller Bücher der Bibliothek als Html-Datei ausgeben
• eine Liste aller Bücher der Bibliothek als csv-Datei ausgeben
• eine Liste aller Ausleiher/innen auf dem Bildschirm ausgeben
• eine Liste aller Ausleiher/innen als pdf-Datei ausgeben
• eine Liste aller Ausleiher/innen als Html-Datei ausgeben

usw.

Die Lösung des obigen Problems besteht in der Trennung der Aufgaben (separation of concerns): Das Bibliotheksprogramm besitzt eine Klasse Listengenerator, die zur Ausgabe jeder Listenart (Bücherliste, Ausleiherliste, …) je eine Methode besitzt. Dieser Klasse stellen wir ein Objekt (im folgenden kurz: Ausgabeobjekt) zur Verfügung, das sich darum kümmert, in welcher Form die Listen ausgegeben werden (auf dem Bildschirm, als pdf-Datei, …). Damit die Methoden der Klasse Listengenerator dieses Ausgabeobjekt nutzen können, müssen sie „wissen“, welche Methoden es besitzt. Diese Vereinbarung wird in einem Interface getroffen:

interface Ausgeber {
   void schreibeZellwert(String wert);
   void neueZeile();
}

In unserem Fall erwarten wir vom Ausgabeobjekt, dass es Tabellen ausgeben kann. Dazu besitzt es eine Methode zur Ausgabe von Text in einer Tabellenzelle und eine Methode, um eine neue Tabellenzeile zu beginnen.

Mit dem Interface alleine kann man nichts anfangen, denn es besitzt noch keinen Programmcode, der die Aufgaben wirklich erledigen kann. Wir müssen Klassen schreiben, die genau die Methoden besitzen, die das Interface definiert. Man sagt: Diese Klassen implementieren das Interface. Wir beginnen mit einer Klasse, die eine Tabelle auf dem Bildschirm ausgeben kann:

Die Festlegung implements Ausgeber in Zeile 1 bedeutet: „Die Klasse Bildschirmausgeber besitzt alle im Interface Ausgeber definierten Methoden. Lösche im oberen Beispiel mal eine der beiden Methoden der Klasse Bildschirmausgeber raus und schau' Dir an, was passiert!

Wir schreiben weitere Klassen, die das Interface implementieren:

Der Listengenerator soll mit jeder der obigen Ausgabeklassen zusammenarbeiten können. Wir geben ihm daher ein Attribut ausgeber vom Typ Ausgeber. Dieses Attribut kann auf beliebige Objekte zeigen, die das Interface Ausgeber implementieren. Daher lassen sich mit diesem Attribut nur diejenigen Methoden aufrufen, die das Interface Ausgeber definiert.
Be Wir lassen das Attribut ausgeber zuerst auf ein Objekt der Klasse Bildschirmausgeber zeigen und rufen die Methode schreibeBücherListe() auf. Anschließend wiederholen wir dasselbe mit den beiden anderen Ausgeber-Klassen.

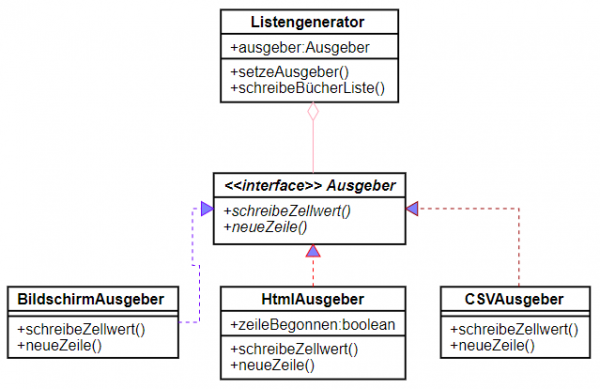Ein Interface sieht im UML-Diagramm aus wie eine Klassenkarte, der Bezeichner ist jedoch kursiv geschrieben und durch ein vorangestelltes «interface» als solches gekennzeichnet. Dass eine Klasse ein Interface implementiert, kennzeichnet man im UML-Diagramm durch eine gestrichelte Verbindungslinie, die beim Interface in ein Dreieck mündet.

Schreibe eine Klasse JSonAusgeber, die das Interface Ausgeber implementiert und Tabellen im JSon-Format als Liste ausgibt, also so:

[ 'Zeile1, Spalte1', 'Zeile1, Spalte2' ],
[ 'Zeile2, Spalte1', 'Zeile2, Spalte2' ]

Schreibe ein Programm, dass ständig die seit dem Programmstart vergangene Zeit in Minuten und Sekunden (Beispiel: 03:12) anzeigt.
Tipp: Die Methode SystemTools.clearScreen() löscht den Textausgabebereich.

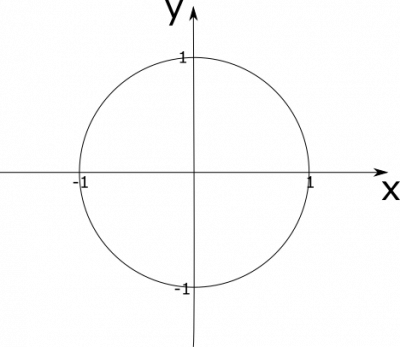Wir wollen Inhalte ebener, begrenzter Flächen mithilfe der Monte-Carlo-Simulation berechnen. Am Beispiel der Fläche des Einheitskreises (Kreis um den Punkt (0,0) mit Radius 1) erkläre ich Dir, wie das geht.

In diesem Fall wählen wir das Rechteck, das von $x_{min} = -1$, $x_{max} = 1$, $y_{min} = -1$ und $y_{max} = 1$ begrenzt ist.

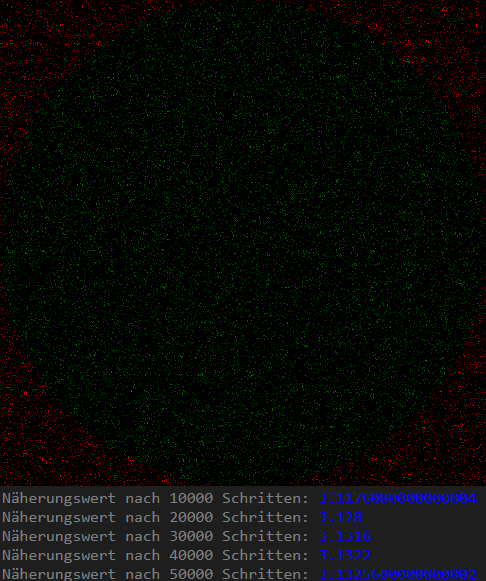
Wie das aussieht, siehst Du an der Grafik rechts oben. Ein Teil der Punkte liegt in der zu bestimmenden Fläche (grün), ein Teil außerhalb (rot).

Angenommen, wir haben 10000 Punkte gesetzt, davon liegen 7894 im Einheitskreis. Dann lässt sich ein guter Näherungswert für seinen Flächeninhalt so berechnen: $$ Fläche_{Kreis} = \frac{Fläche_{Rechteck}}{10000} \cdot 7894 = \frac{(x_{max} -x_{min}) \cdot (y_{max} -y_{min})}{10000}\cdot 7894 = \frac{4}{10000}\cdot 7894 \approx 3,1576$$

Da die Punkte zufällig gewählt sind, ergibt sich bei jedem Programmablauf ein anderer Wert für die Kreisfläche. Dieser nähert sich bei zunehmender Punktezahl aber mit immer größerer Wahrscheinlichkeit immer mehr dem exakten Wert ($\pi\cdot r^2 = \pi\cdot 1^2\approx 3,141592$) an. Meldung eines beispielhaften Programmablaufs:

• Nach 10000 Schritten liegen 7839 Punkte in der Fläche. Näherungswert nach 10000 Schritten: 3.1356
• Nach 20000 Schritten liegen 15674 Punkte in der Fläche. Näherungswert nach 20000 Schritten: 3.1348000000000003
• Nach 30000 Schritten liegen 23431 Punkte in der Fläche. Näherungswert nach 30000 Schritten: 3.1241333333333334
• Nach 40000 Schritten liegen 31303 Punkte in der Fläche. Näherungswert nach 40000 Schritten: 3.1303
• Nach 50000 Schritten liegen 39170 Punkte in der Fläche. Näherungswert nach 50000 Schritten: 3.1336000000000004

Die Klasse Flächenberechner verfügt über eine Methode berechneFlächenInhalt(Fläche fläche), die Mittels der Monte-Carlo-Methode den Flächeninhalt der als Parameter übergebenen Fläche berechnen kann. Aber wie soll so ein Fläche-Objekt beschaffen sein, d.h. welche Methoden soll es haben?
Überlegen wir, was wir zur Durchführung der Monte-Carlo-Methode benötigen:

• Wir müssen ein achsenparalleles Rechteck um die Fläche ziehen, brauchen also die Werte $x_{min}$, $x_{max}$, $y_{min}$ und $y_{max}$.
• Für jeden der zufällig bestimmten Punkte im Rechteck müssen wir wissen, ob er in der zu messenden Fläche liegt oder nicht.

Diese Anforderungen formulieren wir als Interface:

interface Fläche {
   public boolean punktLiegtDrin(double x, double y);
   public double getXMin();
   public double getXMax();
   public double getYMin();
   public double getYMax();
}

Wir schreiben eine Klasse Einheitskreis, die das Interface implementiert und dem Einheitskreis entspricht.

Übernimm den Code für das Interface Fläche und die Klasse Flächenberechner und programmiere dazu

• a) Eine Klasse Dreieck, die das Dreieck mit den Eckpunkten $(0,0)$, $(0,1)$ und $(1,0)$ repräsentiert.
• b) Eine Klasse Sinus, die dem Flächenstück unter dem ersten „Buckel“ der Sinusfunktion entspricht.
  Berechne mit Hilfe dieser beiden Klassen näherungsweise den jeweiligen Flächeninhalt.
• c) Für die Interessierten: Versuche, die Klasse Flächenberechner zu verstehen!

Hier geht's zur Lösung.